在几何学中,直角三角形是一个基础且常见的几何形状,而其中的90°直角三角形更是被广泛应用于各个领域。本文将详细介绍如何计算90°直角三角形的斜边长度,帮助读者更好地理解和运用这一几何概念。
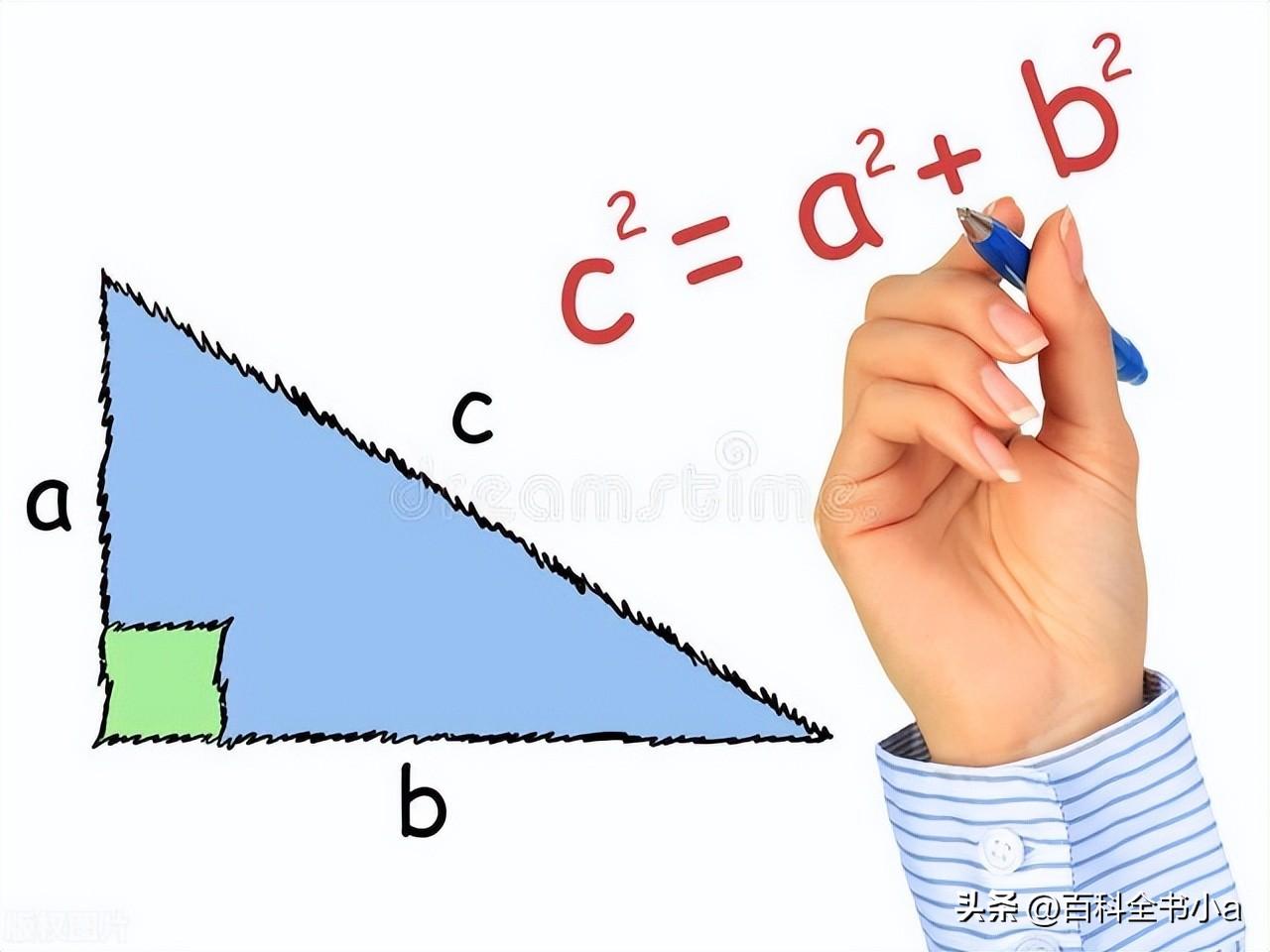
1. 什么是90°直角三角形?
90°直角三角形,又称为直角三角形,是一种其中一个角度为90°的三角形。在这种三角形中,边长相对于直角的两条边被称为直角边,而边长位于直角对面的边被称为斜边。

2. 毕达哥拉斯定理
要计算90°直角三角形的斜边长度,可以使用毕达哥拉斯定理。该定理指出,在一个直角三角形中,直角边的平方和等于斜边的平方。换句话说,对于一个直角三角形,如果已知两条直角边的长度,可以通过以下公式来计算斜边的长度:
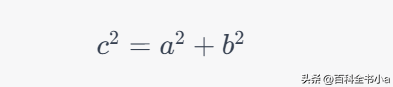
其中,c表示斜边的长度,a 和b分别表示两条直角边的长度。
3. 例子演示
假设有一个直角三角形,其中直角边 a的长度为3,直角边 b的长度为4,我们可以使用毕达哥拉斯定理来计算斜边 c的长度:
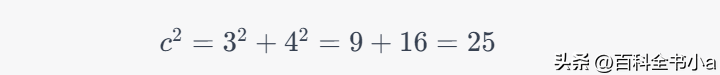
然后,我们可以取平方根来得到斜边的长度:
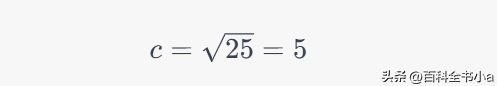
所以,当直角边长度分别为3和4时,斜边的长度为5。
4. 应用领域
90°直角三角形的斜边计算在实际中有广泛的应用。例如,在建筑和工程领域中,我们可以利用这一概念来计算房屋的屋顶倾斜度和斜坡的坡度。在航空和航海领域,这一原理也可以用于导航和测量。
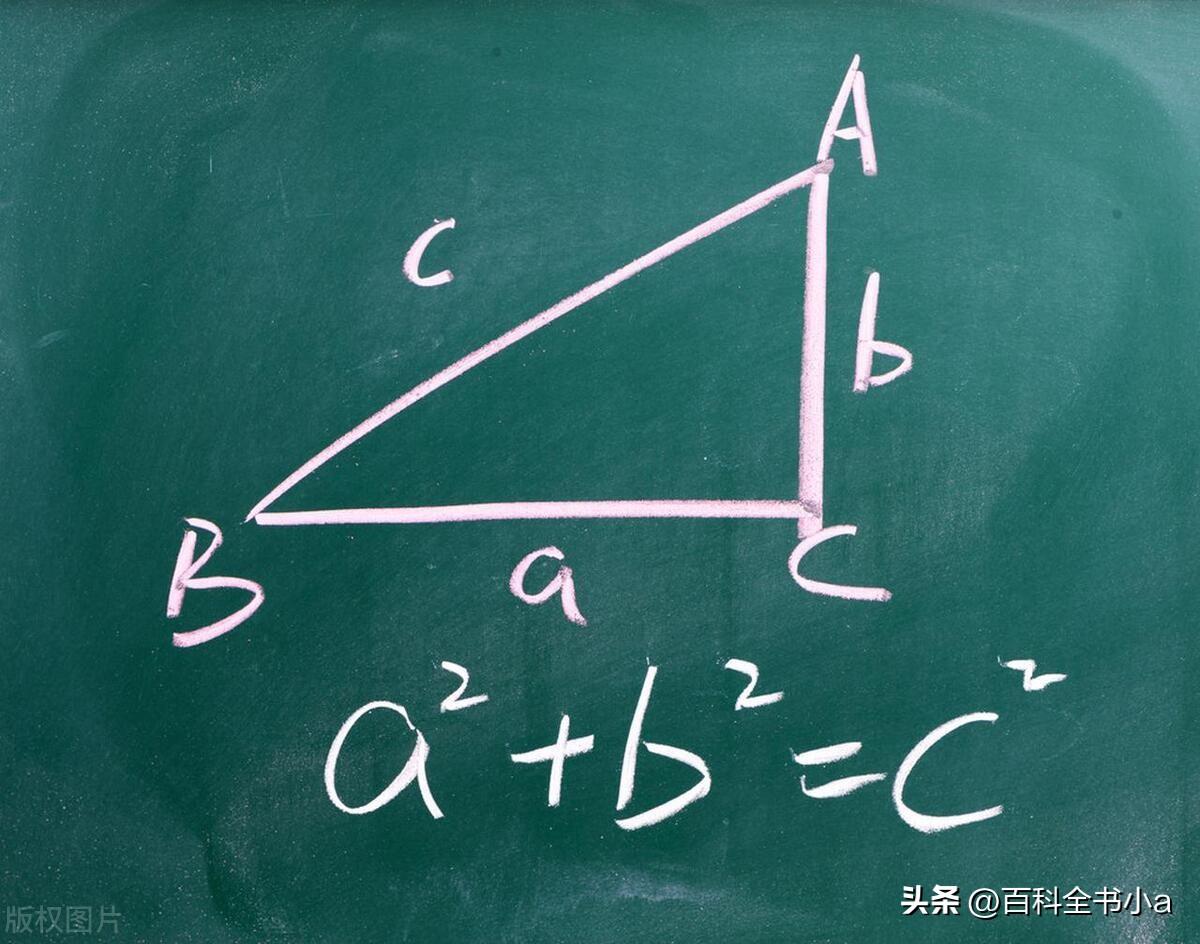
5. 结语
通过毕达哥拉斯定理,我们可以方便地计算90°直角三角形的斜边长度。这一原理在数学和实际应用中都有重要作用,帮助我们解决各种问题。希望本文能够帮助读者更好地理解和运用这一几何概念。






