分享一道求五边形面积的几何综合题,这道题目比较简短,要求的是不规则图形的面积,题目具有一定难度,大家要弄清所给出的条件对于解题有什么作用。此题考查了正方形、三角形与梯形面积公式的灵活运用,以及等积变换的知识。下面,我们就一起来看这道例题吧!
例题:(初中数学综合题)如图,已知四边形ABCD和CGEF是两个正方形,AG和CF相交于H,并且CH等于CF的三分之一,三角形CHG的面积等于6平方厘米,求五边形ABGEF的面积.
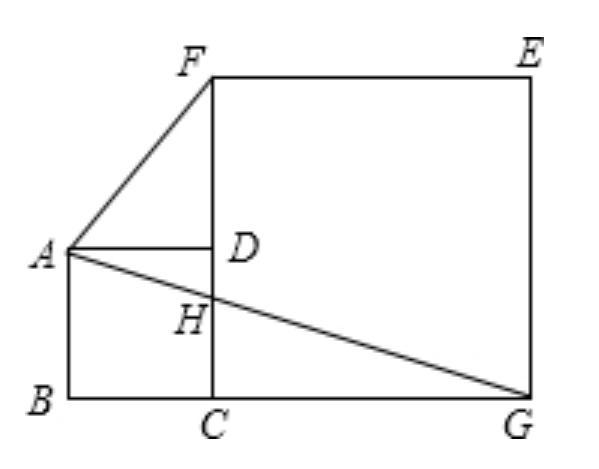
分析:大家想要正确解答一道数学题,必须先将大体思路弄清楚。下面就简单分析一下此题的思路:由四边形ABCD和CGEF是两个正方形,CH=1/3CF,三角形CHG的面积等于6平方厘米,即运用三角形面积公式求得正方形CGEF的边长;由条件易得S△AHF=S△CHG,运用三角形面积公式即可求得正方形ABCD的边长AD;在根据S五边形ABGEF=S正方形CGEF+S四边形ABCF,即可求得结果.
解答:(以下的过程仅供参考,可以部分进行调整,并且可能还有其他不同的解题方法)
∵四边形ABCD和CGEF是两个正方形,
∴AB=BC=CD=AD,FC=CG=GE=FE,∠B=∠FCG=90°,
∵三角形CHG的面积等于6平方厘米,CH=1/3CF,
∴S△CHG=1/2CH·CG
=1/2×1/3CF×CG
=1/6CG·CG=6,
∴CG=6厘米,
即CF=CG=6厘米,
∴CH=1/3CF=2厘米,
∴S正方形CGEF=36平方厘米,
∵S四边形ABCF=1/2(CF+AB)·BC
=1/2CF·BC+1/2AB·BC
=1/2CG·AB+1/2AB·BC
=1/2AB·(CG+BC)=S△ABG,
∴S△AHF=S△CHG,
即1/2HF·AD=6,
∴1/2(CF-CH)·AD=6,
即1/2×(6−2)×AD=6,
∴AD=3厘米,
∴S四边形ABCF=1/2(AB+CF)·BC
=1/2×(3+6)×3
=13.5(平方厘米)
∴S五边形ABGEF=S正方形CGEF+S四边形ABCF
=36+13.5=49.5(平方厘米)
(完毕)
这道题考查了图形面积的求法、正方形、三角形与梯形面积公式的灵活运用,以及等积变换的知识,此题难度适中,解答本题的关键是灵活运用面积公式求得正方形的边长。





