
我也会在“学保险”版块单独列出一栏,不定期分享这些内容。
内容简介
●大数法则
●定价的目标
●费率演示
★
一、大数法则
人生,面临着很多严重的风险,如疾病、残疾、失业、死亡...
更令人不安的是没有人能预知自己何时会生病、何时会死亡,除非是早有预谋。
个人充满了不确定性,然而群体却不是。
他们发生风险的背后总是遵从着一定的规律,人数增多,实际情况和我们预估情况的偏差越小。比如1000人,偏差在±5%的概率为18.2%,5000人,为39.0%,100万人,为99.99%。
因此,我们可以较准确的估计,100万的男性被保人,大约有783人,将于30岁这一年里罹患6种常见的重疾之一,其中有204个人将因病逝世。(数据源于中国人身保险业重大疾病经验发生率表(2006-2010))
这被称为为保险的大数法则。
保险的本质就是通过运用大数法则,集合风险,分散风险。
而保险公司在实际的运营中,也必须去遵循大数定律,发售的保险产品尽量包含更多的同类型被保人,来保证预估的赔付稳定。这一点上,大公司更有优势,而小公司为了分散风险,则可以采取再保险的方式。
二、定价的目标
大数法则的存在,使得保险成为了可能。
然而涉及到具体的定价,保险公司始终致力追求以下三个目标:
1、费率充足
保险合同一旦订立,保险公司就承诺当某类事情发生时,给付保险金。
这笔保险金,可以看作保险公司欠的一笔债,为了保证还上这笔债,保险公司必须要收取足够的保费。
一旦费率不充足,就需要保险公司从自己的盈余中垫付保险金,更有甚者会产生偿付危机。
我国对保险公司的偿付能力也进行了严格的监管,以避免保险公司激进的定价策略导致客户利益受损。
2、费率公平
保险公司每发售一类产品,都在无形中将被保人分成了不同的组别,比如根据年龄和性别将30岁男性和31岁男性划成不同的组别,也可以按照是否吸烟划成吸烟与不吸烟的组别。
根据统计的数据,不同组别的死亡率有所差别,势必要对他们收取不同的保费,以符合潜在的期望损失。
如果收取的保费不能反映真实的损失率,那么补贴情形就产生了:对一个组别收取的保费过高,以弥补另一个组别收取的过低保费。
这就是不公平。
极端情况下,补贴情形会导致大量逆选择发生,从而使得保险系统崩溃。
另外,在现实中,我们并不能做到完全意义上的公平,还有很多因素是没有数据可供参考的,比如基因问题。当然,在中国以基因来区别定价是违法的。
核保是实现费率公平的重要手段,通过年龄、性别、健康情况等因素将同一类型的准被保人分为一组,以达到一定程度的公平。
我们知道,分组越细致,这种公平程度更明显,然而越细致的分组对应的是每组更少的被保人,这显然与保险公司追求大数法则的目标相违背。
这也是为什么保险公司可以出一款承保Ⅱ型糖尿病人的保险、却不敢出一款承保Ⅰ型糖尿病人的保险原因之一(根据数据统计,中国糖尿病患者超过1亿,其中90%为Ⅱ型糖尿病人)。
3、费率不过高
保险的费率与对应的给付相比较而言,不应过高。
如果将费率充足视为费率下限,则费率不过高是费率上限。
在中国,监管通过人身险精算规定对保险的费率上限做了一定程度的限制。除了这些强制性规定以外,更多制约保险公司费率上限的来源于市场因素:竞争。
一个较高的费率在一个公开透明的保险市场是没有竞争力的,而目前中国的保险市场并未完全的公开透明,高费率仍然有着一席之地。
三、费率演示
接下来我们将要进行一些初级的保险精算,了解一下人寿保险的净保费是如何计算出来的。
保费的计算主要考虑以下4种因素:
●承保事件发生的概率
●资金的时间价值
●承诺的给付
●包括费用、税务、利润和意外事件在内的附加费用
如果计算保费时,仅考虑前3项,计算得出的称为净保费,加上第4项就称为毛保费,也就是保险公司向我们收取的保费:
净保费+附加费用=毛保费
接下来进行演示。
1、仅考虑概率
根据美国1980CSO生命表,30岁男性的死亡率为每1000人死亡1.73人。
如果现在有100000名男性,每人投保1000元保额的一年期定期寿险,那么保险公司该收取多少保费呢?
一共是100000人,预期死亡173人,累计赔付:173*1000=173000元。
因此保险公司只需要向每人收取173000/100000=1.73元,就足够支付赔付费用。
这种计算仅考虑了死亡率和给付值,有助于我们理解大数法则,然而真正的净保费计算还需要考虑资金的时间价值。
2、年可续定期寿险
保险公司收取的保费,在扣除一定的费用后,会用于投资获益。
保险公司在计算保费时,往往会预估一个投资收益的利率,也常被称为预定利率。
我们将以5%的预定利率来计算净保费。
在这里,我们将要用到两个重要的假设:
1)保费的收取都在保单年度初(很实际的假设)
2)死亡的给付都在保单年度末(不合实际的假设,这样的假设会给保险公司带来一定的亏损,保险公司往往在费用附加公式和计息时点上做一些小的调整来纠正损失)
基于这样的假设,对于年初收取的保费,保险公司有整整一年的时间去投资获益。
针对上文提及的问题,为了支付年末赔付的173000元,年初只需要收费1730000*(1/1.05)=164762元即可,投资收益可以创造另外的8238元。
同时,我们发现,保险公司不需向每人收取1.73的保费,只需1.65元,这样我们的保费就降低了,或者用专业术语来说:我们的保费被折现了,折现后的数值也被称为现值。
也有人说,预定利率越高,保费越低。
这句话并不完全正确,预定利率只能决定净保费的高低,而保险公司收取的是毛保费,如果定价时保险公司的成本和预留利润较高,即使预定利率高,毛保费也未必便宜。
另外,我国对保险公司的预定利率实行了严格的监管政策,比如之前银保监会约谈数家保险公司要求停止开发并下架4.025%预定利率定价的产品。
上面计算的最简单的是年可续定期寿险的净保费,也就是常说的“交一年保一年”的定期寿险,保险市场上还有不同的缴费方法,如趸交,水平保费,还有万能寿险这样的灵活缴费方式。
3、趸交终身寿险
趸交保费,意为一次性缴纳所有的保费。
因为在购买保险之后,大多数被保人不会很快死亡,趸交寿险保费相对于年可续寿险保费,保险公司有着更多的时间和本金去投资获益,因此在净保费的计算中,投保人缴纳的净保费更低。
为了简化计算,假设有100000名95岁男性,购买了保额为1000元的趸交终身寿险保单,保险公司该向每个被保人收取多少的趸交保费呢?
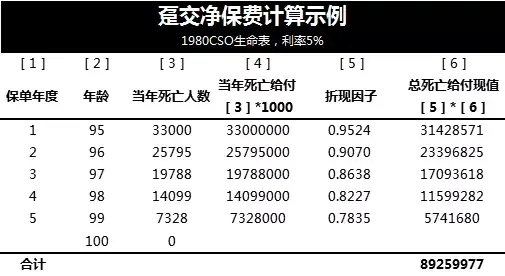
1980CSO生命表仅计算到100岁,也就是假设所有人都在100岁时死亡。
第三列的死亡人数可以通过生命表计算得出,是已知的,第4列死亡给付等于死亡人数*保额(1000)。
在考虑5%的投资收益之后,实际的现值是第6列的数据,把5个年度的死亡给付加总,就能得到总死亡给付的现值。
而总死亡给付现值等于我们需要收取的趸交净保费,因此每个人需要支付的保费为:89259977/100000=892.6元。
在趸交净保费的基础上,再加上附加费用得出的总保费也许会超过保额1000元,这个现象被称为:保费倒挂,指的是保费大于保额的情形。此时不能视作我们购买了保险,我们只是和保险公司做了简单的资金交换而已。
因此在逻辑上,没有人愿意在这个年龄去购买保险。
之所以会产生这样的现象,是因为这个年龄的死亡率太高,只有当损失概率相对较低,在纯粹的损失成本加上附加费用,保险计划才可行。
趸交保费,在现实中并不常见,不是每个人都有能力或者说愿意支付一笔大额的保费,他们更喜欢分期付款,即水平保费的形式。
4、水平保费终身寿险
同样举上面95岁男性的例子,如果这次换成5年缴费的水平保费,每个人的保费又该是多少?
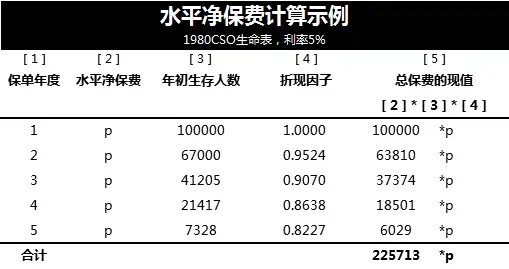
我们假设水平净保费为p,第三列是每个保单年度初仍然生存的人数;
第四列是折现因子,需注意的是第一年的折现因子为1,因为我们假设了保费收取是在保单年初。而上述趸交净保费所折现的不是保费而是死亡给付值,因此第一年的折现因子是0.9524。
第五列是总保费的现值,即2、3、4列的乘积。
我们在上文已经计算过死亡给付的总和:89259977,因此89259977=225713*p,p=395.46,这就是水平净保费的值。
这里我们发现了一个现象:水平净保费的5倍,即395.46*5远远大于趸交净保费892.6.
这是因为相对于趸交净保费,水平净保费的用于投资收益的本金和时间要小的多。另外,水平净保费只能从那些仍然活着的人处收取。
换言之,在水平净保费的计算中,同时对死亡率和利率进行了折算。
实际上,无论是趸交、10年交还是30年交,都遵循着同样的规则:未来给付的现值等于未来总保费的现值,用保险精算公式表示为:
PVFB=PVFP
所谓万变不离其宗,用在这里也再合适不过了。
四、写在最后
上文提及的净保费计算不过是保险精算的一点皮毛而已,真正的计算需要考虑更多的因素,还需要运用各种模型对假设的保费予以测试,以达到保险公司预期的各项目标。
由此而言,精算是一个庞大而繁杂的工作,而精算师也是非常人能够担当的职业,可敬可佩。
随着科技进步,这些精算工作大多可以交由计算机处理,但对于从事保险行业的人来说,了解背后的原理对我们理解产品更替、理解保险市场的变化无疑是重要的。





