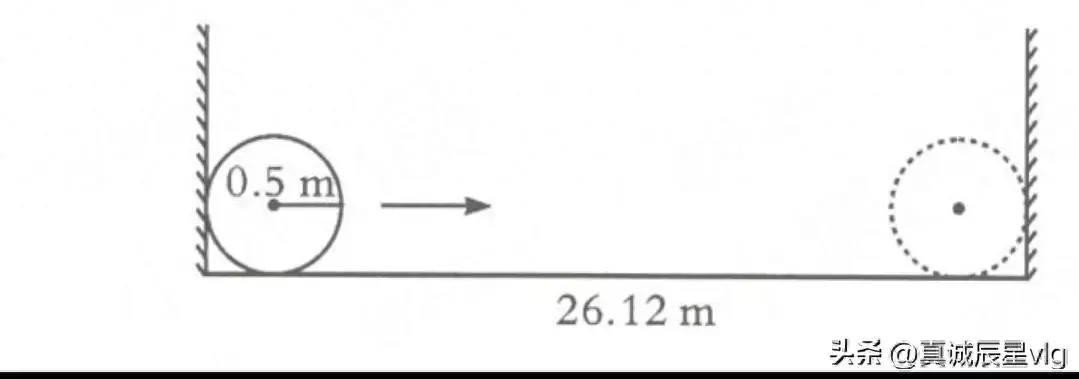
1、如图,底面半径为0.5m的油桶在两侧墙内滚动,两墙之间的距离为26.12 m,油桶从墙的一侧滚到另一侧要滚多少圈?
思路导航
由图可知,从墙一侧滚到另一侧只需要滚动(26.12-0.5×2)m,可以通过计算两个圆心之间的距离得到;再根据圆的周长公式计算出圆周长,总距离除以周长就是所求的圈数。
解答
①滚动的距离:
26. 12-0. 5×2
=26.12-1
=25.12(m)
②圆的周长:
3.14×0.5×2=3.14(m)
③圈数:
25.12÷3.14=8(圈)
答:油桶从墙的一侧滚到另一侧要滚8圈。
2、如图,地面上平躺着一个半径为0.5米的球,如果要将这个球滚到墙边,需要转动几圈?

思路导航:
由题意可知,当球靠墙时球的着地点距墙0.5米(也就是球的半径)
,首先根据圆的周长公式: c=2πr,求出球转动一周的距离,用16.2减去0.5的差除以球转动一周的距离即可求出需要转动的圈数。
解答
①球滚动的距离:
16.2-0.5=15.7(米)
②滚动一周的距离:
3.14×0.5×2=3.14(米)
③周数:
15.7÷3.14=5 (圈)
答:需要转动5圈。
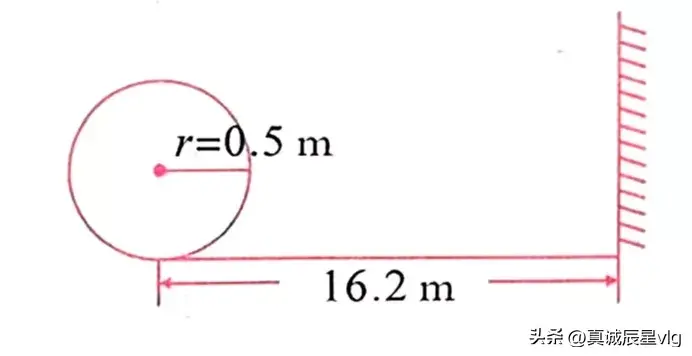
3、如图,“将一个半径为0.5 m的铁环推到与它相距16.2 m的墙边,正好转动5周。”你觉得这个说法对吗?试通过计算说明。
思路导航:
由图可知,铁环的半径为0.5 m,铁环与墙边的距离为16.2m。先求出铁环转一周移动的距离,也就是求出铁环的周长,再算出铁环转动5周移动的距离,加上一个半径的长度0.5 m 正好是16.2 m。
解法一
①5周的长度:
3.14X0.5X2X5=15.7(m)
②总长度
15.7+0.5=16.2(米)
解法二
(16.2-0.5)÷(3.14×0.5×2)=5(周)
答:这个说法对。





